Graph Embedding
Introduction
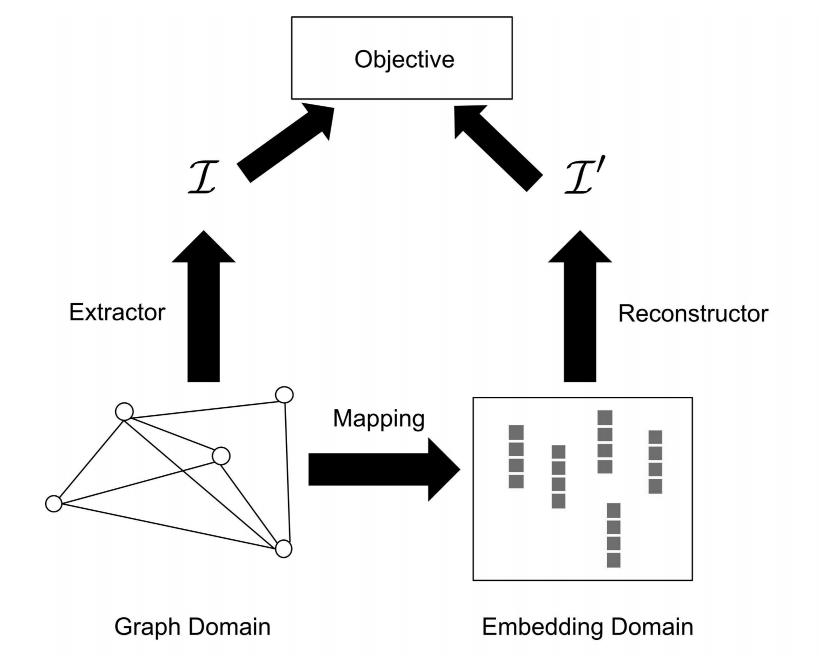
Graph embedding aims to map each node in a given graph into a low dimensional vector representation.
Graph Embedding for Simple Graphs
Graph embedding algorithms for simple graphs that are static, undirected, unsigned, and homogeneous.
Preserving Node Co-occurrence
One of the most popular ways to extract node co-occurrence in a graph is via performing random walks. Nodes are considered similar to each other if they tend to co-occur in these random walks. The mapping function is optimized so that the learned node representations can reconstruct the “similarity” extracted from random walks.
Representative network embedding algorithms preserving node co-occurrence are DeepWalk (Perozzi et al., 2014) and node2vec (Grover and Leskovec, 2016) and LINE (Tang et al., 2015).
Mapping Function
A direct way to define the mapping function $f\left(v_i\right)$ is using a lookup table. This means that we retrieve node $v_i$ ‘s embedding $\mathbf{u}_i$ given its index $i$. Specifically, the mapping function is implemented as
where $\mathbf{e}_i \in\{0,1\}^N$ with $N=|\mathcal{V}|$ is the one-hot encoding of the node $v_i$. In particular, $\mathbf{e}_i$ contains a single element $\mathbf{e}_i[i]=1$ and all other elements are 0 . $\mathbf{W}^{N \times d}$ are the embedding parameters to be learned, where $d$ is the dimension of the embedding. The $i$ th row of the matrix $\mathbf{W}$ denotes the representation (or the embedding) of node $v_i$. Hence, the number of parameters in the mapping function is $N \times d$.
Random Walk–Based Co-occurrence Extractor
Given a starting node $v^{(0)}$ in a graph $\mathcal{G}$, we randomly walk to one of its neighbors. We repeat this process from the node until $T$ nodes are visited. This random sequence of visited nodes is a random walk of length $T$ on the graph. We formally define a random walk as follows.
Definition (Random Walk): Let $\mathcal{G}=\{\mathcal{V}, \mathcal{E}\}$ denote a connected graph. We now consider a random walk starting at node $v^{(0)} \in \mathcal{V}$ on the graph $G$. Assume that at the $t$-th step of the random walk, we are at node $v^{(t)}$ and then we proceed with the random walk by choosing the next node according to the following probability:
where $d\left(v^{(t)}\right)$ denotes the degree of node $v^{(t)}$ and $\mathcal{N}\left(v^{(t)}\right)$ is the set of neighbors of $v^{(t)}$. In other words, the next node is randomly selected from the neighbors of the current node following a uniform distribution.
We use a random walk generator to summarize the above process as follows:
where $\mathcal{W}=\left(v^{(0)}, \ldots, v^{(T-1)}\right)$ denotes the generated random walk, where $v^{(0)}$ is the starting node and $T$ is the length of the random walk.
In DeepWalk, a set of short random walks is generated from a given graph, and node co-occurrence is extracted from these random walks.
These random walks can be treated as sentences in an “artifificial language” where the set of nodes V is its vocabulary. The Skip-gram algorithm (Mikolov et al., 2013) in language modeling tries to preserve the information in sentences by capturing the co-occurrence relations between words in these sentences.
For a given center word in a sentence, those words within a certain distance w away from the center word are treated as its “context.” Then the center word is considered to co-occur with all words in its context.